極方程式の視覚化
GeoGebraでは極方程式を扱うためのコマンドがなく、直交座標の方程式に変形しないと描画ができません。 そこで極方程式を入力すると、その概形が描画される教材を作成しました。 Beauty, Rigor, Surpriseを参照しました。
※できないと思っていましたが、調べていると描画する方法がありました。 (sin(2*t);t)のようにセミコロンを使って入力すると極座標と認識されるようです。Polar curves参照
動画とGeoGebraファイル
動画
GeoGebraファイル
作り方
考え方
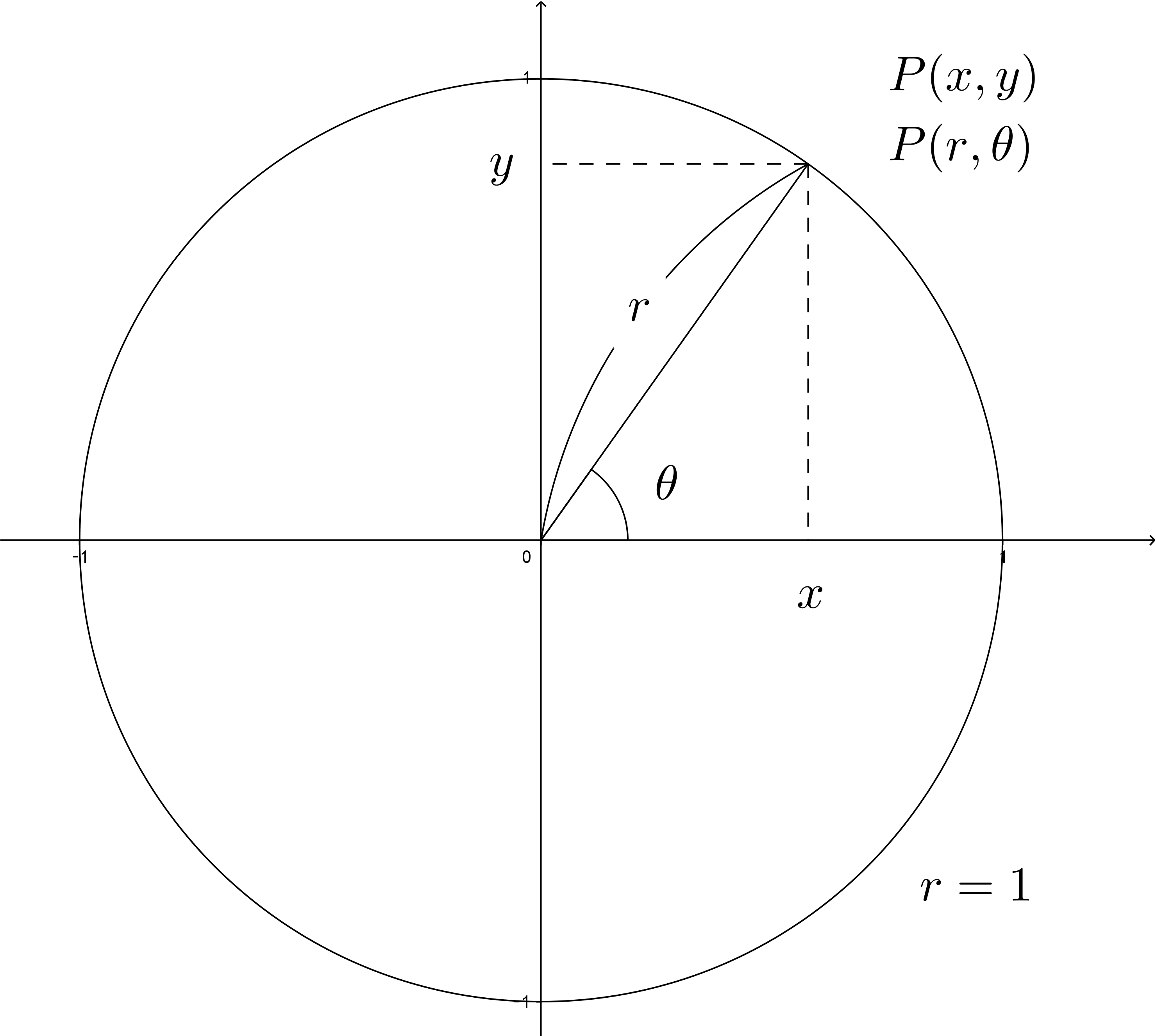
点Pの直交座標が$(x,y)$、極座標を$(r,\theta)$とすると次の関係が成り立ちます。 \begin{cases} x= r\cos\theta \\ y= r\sin\theta \end{cases} さらに極方程式は極座標$(r,\theta)$に関する方程式$r=f(\theta)$のことです。 よって上記の式に$r=f(\theta)$を代入すると以下のようになります。 \begin{cases} x= f(\theta)\cos\theta \\ y= f(\theta)\sin\theta \end{cases} つまり直交座標の$x$座標は$f(\theta)$に$\cos\theta$を掛けたもの、$y$座標は$f(\theta)$に$\sin\theta$を掛けたもので求めることができます。これを利用していきます。
手順
- 変数と入力ボックスを用意する
- Curveコマンドを使って、曲線を描く
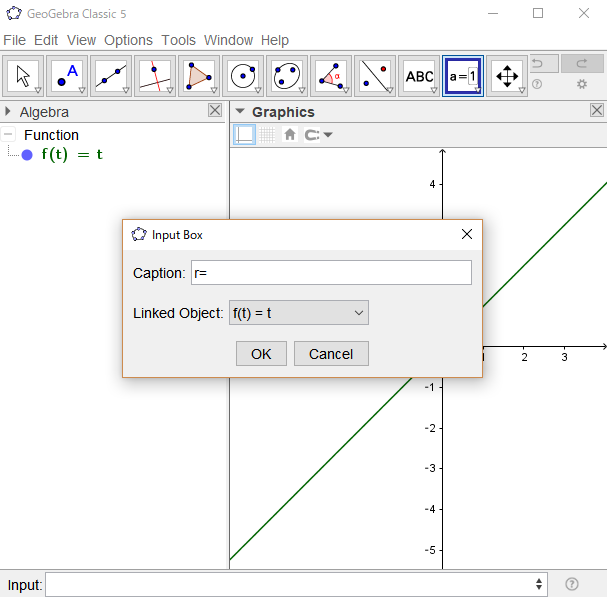
今回は$\theta$ではなくtとします。最初に入力バーに"f(t)=t"と入力して関数を作ります。
次に適当な場所に入力ボックスを作り、見出しを"r="、リンクするオブジェクトを"f(t)"とします。
作れたら、入力ボックスの値を色々と変えて、f(t)と対応しているかを確かめてください。
入力バーに"Curve[f(t)*cos(t),f(t)*sin(t),t,0,2π]"と入力します。すると線が描かれると思います。
試しに"2"などの定数を入れてみてください。すると円が描かれると思います。
Curveコマンドは範囲を与え、媒介変数表示を与えると、曲線を返すコマンドです。第1,2引数が媒介変数表示、第3引数が変数、第4,5引数が範囲です。

まとめ
即時フィードバックで概形が現れると、生徒は自分の予想を確かめやすくなります。 極方程式は意味を理解することが難しいことがあるので、この教材はそのような場合に使っていただければと思います。