OUTLINE ( -> Japanese)
What is PointLine?
PointLine is a product of the Ahara Laboratory, Department of Frontier Media Science (FMS), Faculty of Interdisciplinary Mathematical Sciences, Meiji University. It is an interactive software that allows users to draw plane geometry on the screen and transform it afterward while keeping the drawing procedure.
Similar software includes GeoGebra and Cinderella.
What is the difference from GeoGebra and Cinderella?
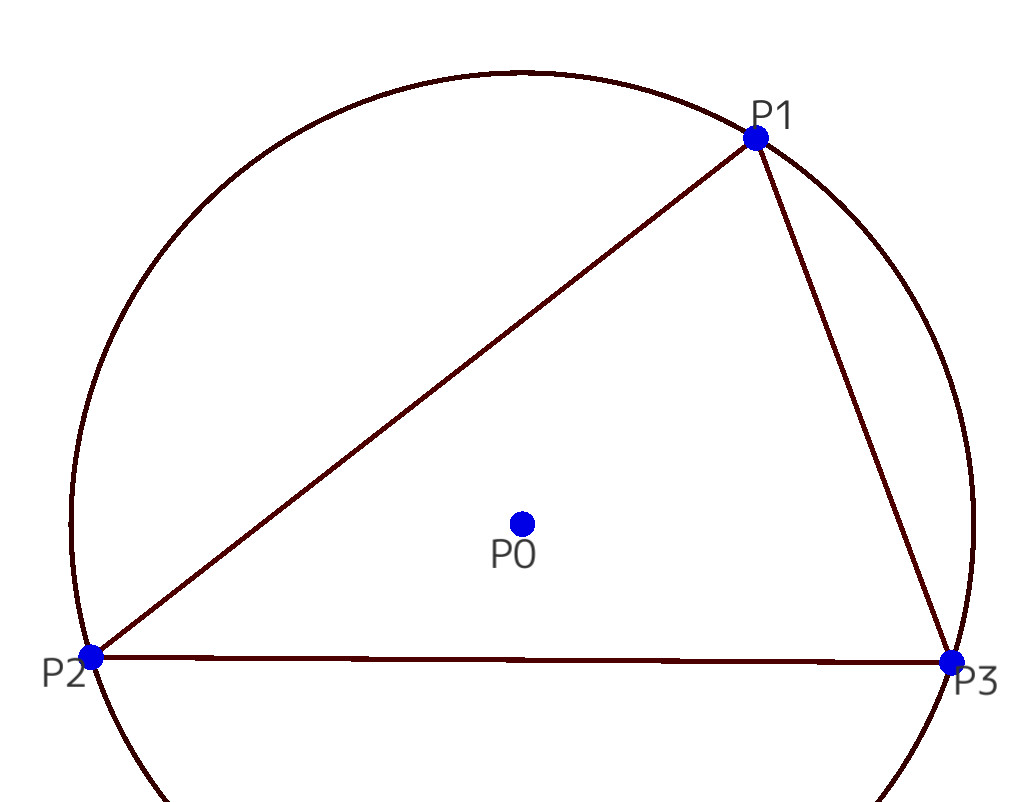
Constructing geometrical figures involves a process called the 'constructing procedure.' In other words, in traditional software, a diagram is established according to a specific procedure using geometrical tools such as those rulers and compasses can do. For example, to find the center of the circumscribed circle from a triangle, one would plot the perpendicular bisectors of each side and then plot their intersections.
In PointLine, we implement the geometric tools by convergence through iteration of Markov processes. This approach makes all drawing tools "bidirectional."
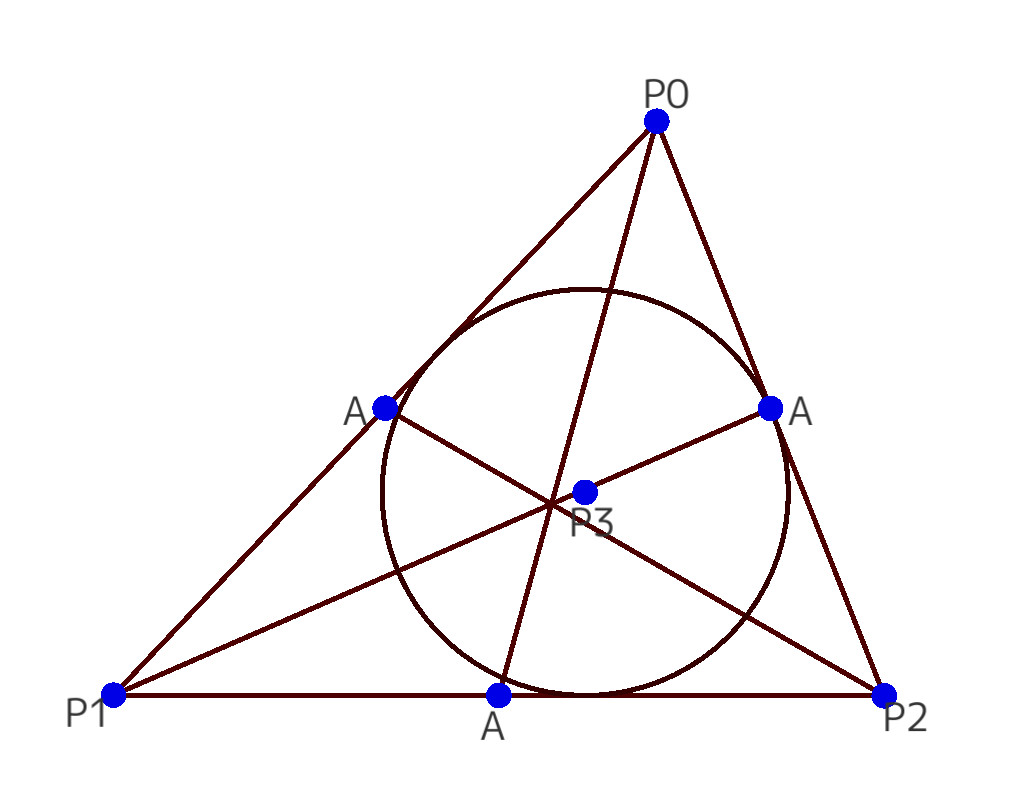
For example, if you want to draw a triangle and the circumcircle, are the two ways "to draw a triangle and draw the circumscribed circle" and "to draw a circle and draw a triangle with three vertices on the circle" the same or different? In traditional software such as GeoGebra, they are two separate drawings because the drawing tool involves the subordination of geometric elements such as vertices and circles."
In PointLine, on the other hand, the drawing tools are bidirectional, so the two drawings are identical. Using iterations of Markov processes gives us a brand-new algorithm here. In addition, there remain open mathematical problems of whether iterations of Markov processes always converge."
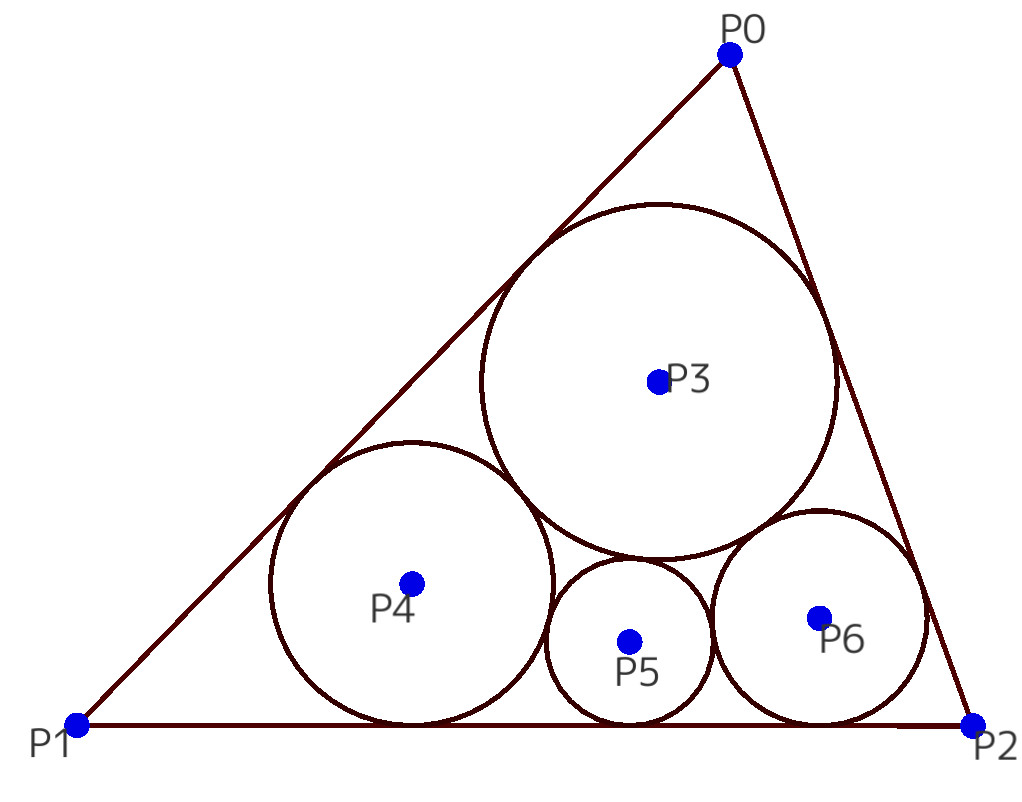
We are allowed to add a geometrical condition in a finishing construction.
The elements of constructing are "vertices," "lines (line segments)," and "circles." PointLine allows you to add conditions such as "a vertex is on a line," "two lines are orthogonal," or "a circle and a line are tangent" after drawing these elements on the screen. This specification means that after drawing a triangle, you can add or remove conditions such as "What shape will the figure have if the first triangle is an isosceles triangle," "What if the first triangle is a right triangle," "What happens if the lengths of the sides are not equal," and so on.
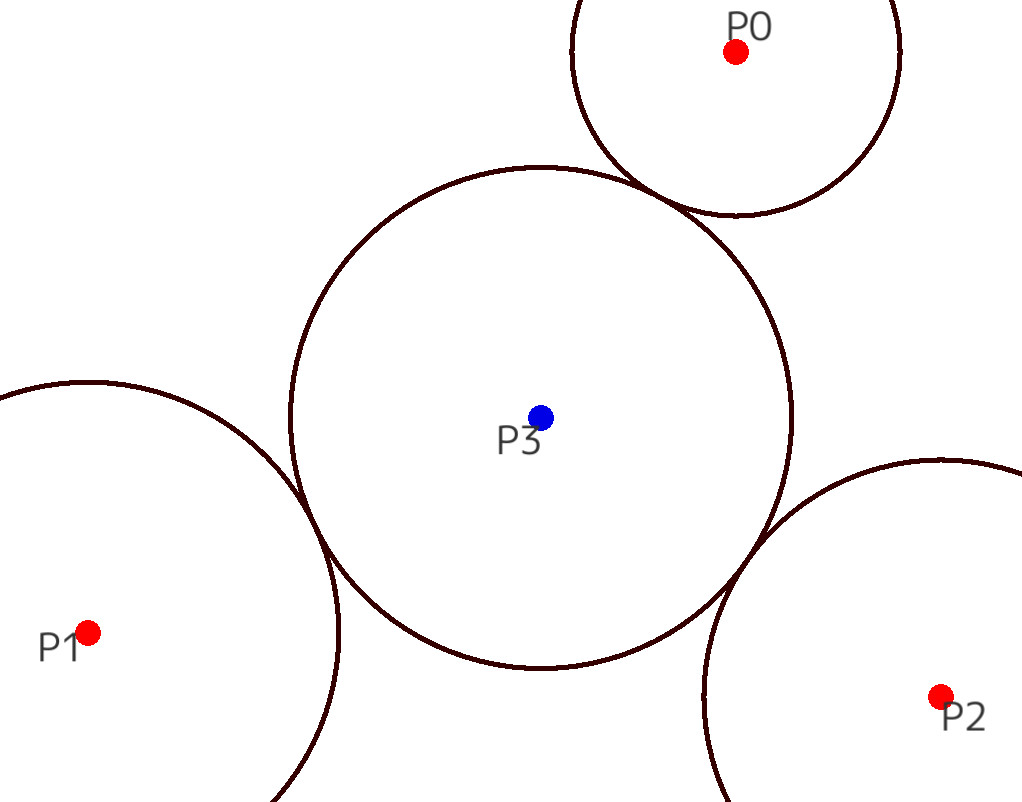
We can make a figure of a difficult consturction
Most GDS (dynamic geometry software) is designed for constructing a geometrical figure with a compass and ruler. Imagine you have a diagram you want to draw, and you do not know how to do it. Thus, it is impossible to draw the diagram. For example, drawing a circle circumscribed by all three given and fixed circles, as shown in the figure on the left, requires a rather complicated construction knowledge. What do you do in such a situation? With PointLine, it is enough for you to draw circles independently once and later to add tangency conditions to other given circles.
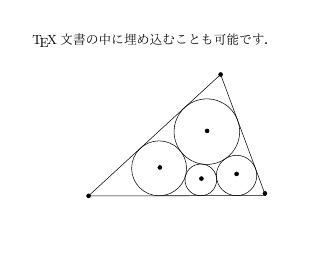
We are allowed to get a TeX file.
We can use the figure in PointLine as a figure in a TeX document. Indeed the figure in PointLine is saved as a Tikz file and it is easy to insert it into a TeX file.
Python verion 'PyPointLine'.
PointLine provides a mathematical problem: whether Markov processes between geometric elements converge by iteration. Open source in Python is available for this research.
https://github.com/aharalabMeiji/PyPointLine
